Hazardní hry › Pravděpodobnost › Definice pravděpodobnosti

Definice pravděpodobnosti

Existují čtyři základní definice pravděpodobnosti – klasická (Laplaceova), geometrická, statistická a axiomatická.

Základní pojmy

Náhodným pokusem rozumíme takový pokus, jehož výsledek závisí na náhodě a který můžeme za stejných podmínek opakovat libovolně mnohokrát.

Z toho vyplývá, že náhodný pokus musí mít alespoň dva různé výsledky, neboť v opačném případě bychom nemohli tvrdit, že výsledek závisí na náhodě. Současně předpokládáme, že náhodný pokus může mít pouze jeden výsledek.

Výsledek náhodného pokusu nazýváme elementární jev. Množinu S všech elementárních jevů nazýváme základní prostor. Libovolnou podmnožinu A základního prostoru S nazýváme náhodný jev.

Klasická definice pravděpodobnosti

Klasická definice pravděpodobnosti (Laplaceova) vychází ze třech předpokladů, resp. požadavků kladených na náhodný pokus: 1. počet všech možných výsledků je konečný, 2. všechny výsledky jsou stejně možné a 3. všechny výsledky se vzájemně vylučují.

Nechť náhodný pokus se základním prostorem S má konečný počet výsledků n (n je z množiny všech přirozených čísel N) a nechť každý elementární jev má stejnou možnost nastat po vykonání náhodného pokusu. Nechť A je libovolný náhodný jev, tvořený m elementárními jevy. Potom pravděpodobnost P(A) náhodného jevu A definujeme jako podíl:

kde:
m je počet případů příznivých a
n je počet všech možných případů.

Geometrická definice pravděpodobnosti

Definice geometrické pravděpodobnosti je založena na porovnávání ploch, objemů nebo délek různých geometrických útvarů. Nechť náhodný pokus se základním prostorem S má nekonečně mnoho výsledků a každý z těchto výsledků má stejnou možnost nastat. Potom pravděpodobnost P(A) náhodného jevu A z množiny S definujeme jako podíl:

kde:
m(A) je míra geometrického útvaru, reprezentujícího náhodný jev A a
m(S) je míra geometrického útvaru, reprezentujícího základní prostor S.

Statistická definice pravděpodobnosti

Uvažujeme náhodný pokus P a sledujme náhodný jev A, který může nastat po provedení pokusu P. Zopakujme náhodný pokus P n-krát za stejných podmínek. Nechť m udává, kolikrát v dané sérii pokusů nastal jev A. Tento poměr nazýváme relativní četností. Jestliže s rostoucím počtem opakování pokusu se relativní četnost blíží určitému číslu, potom toto číslo můžeme považovat za statistickou pravděpodobnost daného jevu. Statistickou pravděpodobnost jevu A tak definujeme jako limitu podílu:

Axiomatická definice pravděpodobnosti

Axiom (pochází z řeckého slova axióma = to, co se uznává) je tvrzení, které se předem (a priori) pokládá za platné a tudíž se nedokazuje.

Nechť φ je pole náhodných jevů. Libovolnou reálnou množinovou funkci P, definovanou na φ, nazveme pravděpodobností, jestliže platí:

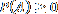, tzn., že pravděpodobnost každého jevu je nezáporná,
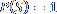, tzn., že pravděpodobnost jistého jevu je 1,
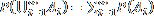, tzn., že pravděpodobnost sjednocení vzájemně se vylučujících jevů (po dvou disjunktních jevů) je rovna součtu jejich pravděpodobností.

Z uvedených axiomů vyplývá, že:

pravděpodobnost je číslo v intervalu <0, 1>, kde 0 je jev nemožný a 1 jev jistý,
pravděpodobnost opačného jevu je doplněk do jedné,
pravděpodobnost sjednocení navzájem se vylučujících (disjunktních) jevů je rovna součtu jejich pravděpodobností atd.

Sdílej tuto stránku na Facebooku