Aritmetický, vážený, geometrický a harmonický průměr
Průměr je známá statistická veličina, s kterou se člověk setkává už od základní školy. Kdo by neuměl sečíst všechny hodnoty a vydělit je jejich počtem? Mohou však i nastat trochu složitější případy (vážený a geometrický průměr). Navíc zásadní otázkou pro statistika je, zdali má vůbec průměr použít, nebo namísto něj vzít v úvahu raději modus či medián.
Když se řekne průměr, většinou máme na mysli právě uvedený aritmetický průměr. Jen menší potíže může činit, pokud máme údaje určitým způsobem zatříděny (řečeno jazykem statistiky) do tabulky četností, například víme-li, že určitá hodnota se vyskytla 5krát, další hodnota 8krát atd., anebo pokud mají různé hodnoty různou váhu. V tomto případě použijeme vážený průměr. Méně známé a rovněž všeobecně méně používané jsou geometrický průměr a harmonický průměr. Uvedeme si vzorce a vše si jako tradičně blíže vysvětlíme na příkladech.
Aritmetický průměr
Aritmetický průměr má výhodu v tom, že bere v úvahu všechny hodnoty a jistým způsobem jej můžeme použít jako (jediného) reprezentanta všech hodnot. Na druhou strany má i své nevýhody, především v tom, že byť ojedinělé extrémně velké či malé hodnoty mohou průměr značně zkreslit. Například máte-li čtyři studenty se známkami 1, 1, 1, 5, průměrná známka je 8 / 4 = 2, což může zakrýt, že máme tři vynikající studenty a jednoho flákače (nebo se prostě jen nezadařilo).
Podobné rozdíly bychom mohli nalézt třeba u mzdového ohodnocení. Budete-li mít několik dělníků se mzdou 10 tis. Kč a dva manažery se mzdou 100 tis. Kč, výsledná průměrná mzda může být zkreslena. Nic nesoudíme, ba naopak, komu čest, tomu čest. Z pohledu statistiky je důležité, kdo a pro jaký účel se statistickou veličinou (zde s průměrem) pracuje. Především jde o to, aby byla reprezentativním ukazatelem. Někdy může být vhodnější použít medián nebo modus.
Vzorec pro aritmetický průměr
Nejčastěji se používá zkrácený zápis se sumou (označena řeckým písmenem ∑ – velká sigma):
![]()
Suma sčítá všechny hodnoty. Ekvivalentně můžeme vzorec pro aritmetický průměr zapsat v rozvinuté formě takto:
![]()
Jestli vás ve vzorcích mate výraz 1/n, tak můžeme říci jen to, že vynásobit něco 1/n je stejné jako vydělit n. Takto se vzorce pro průměr ve statistice prostě zapisují. Sluší se samozřejmě ještě uvést, že ![]() je aritmetický průměr a x1 až xn jsou jednotlivé hodnoty (statistického znaku – opět řečeno jazykem statistiky) a n je celkový počet hodnot.
je aritmetický průměr a x1 až xn jsou jednotlivé hodnoty (statistického znaku – opět řečeno jazykem statistiky) a n je celkový počet hodnot.
Pokud jsou hodnoty zatříděny, tzn., víme kolikrát se která hodnota objevila, vzorec pro průměr je následující:
![]()
kde k je počet tříd a mi je četnost hodnoty xi. Vše bude jasné z následujícího příkladu. A níže také uvidíme, že tento zápis je jen jinou formou váženého průměru, kde jako váhy slouží četnosti.
Příklad
Písemného testu ze statistiky se zúčastnilo dvacet žáků (n = 20) a výsledné známky byly následující (x1 až x20): 3, 2, 1, 2, 3, 4, 5, 2, 3, 2, 2, 3, 3, 4, 5, 1, 2, 1, 3, 3. Jaká je průměrná známka?
Řešení: ∑xi = 3 + 2 + 1 + … = 54, n = 20. ![]() = 54 / 20 = 2,7
= 54 / 20 = 2,7
Nyní bychom mohli dostat stejný úkol s tím rozdílem, že by již někdo provedl statistiku, kolikrát se která známka z testu objevila – viz následující tabulka četností.
| Známka xi | Počet studentů mi |
|---|---|
| 1 | 3 |
| 2 | 6 |
| 3 | 7 |
| 4 | 2 |
| 5 | 2 |
| Celkem (n) | 20 |
To znamená, že údaje byly zatříděny. Počet známek je počet tříd (k = 5), jednotlivé známky 1 až 5 jsou hodnoty x1 až x5 a kolikrát se vyskytly, jsou četnosti m1 až m5. Dosadíme do vzorce:
![]() = (1/20) × (1 × 3 + 2 × 6 + 3 × 7 + 4 × 2 + 5 × 2) = (1/20) × 54 = 2,7
= (1/20) × (1 × 3 + 2 × 6 + 3 × 7 + 4 × 2 + 5 × 2) = (1/20) × 54 = 2,7
Není asi třeba uvádět další příklady, výpočet průměru je poměrně triviální. Tak zkusme jen pár vtipných příkladů. Váš kamarád sní svou i vaši svačinu. V průměru jste měli každý jednu svačinu (0 + 2 = 2 ÷ 2 = 1). To by vás jistě utěšilo. Dále jeden hezký citát říká, že strčíte-li hlavu do mrazáku a nohy si dáte do teplé vody, tak statistik bude hovořit o příjemné průměrné teplotě.
Vážený průměr
Vážený průměr pouze zobecňuje aritmetický průměr. Používá se tam, kde hodnoty (statistického znaku) nemají stejnou váhu. Případně tam, kde již máme hodnoty určitým způsobem zatříděny (viz předchozí příklad), nebo máme-li například spočítat aritmetický průměr z několika (pod)souborů, které mají různý počet hodnot a potřebujeme je sloučit do jedné průměrné hodnoty, která by charakterizovala všechny (pod)soubory.
Vážený průměr používáme na našem webu velmi často. Očekávaná hodnota, pomocí které můžeme určit (ne)výhodnost jakékoliv sázky, není nic jiného než vážený průměr, kde váhami jsou pravděpodobnosti výhry a prohry. O tom bude ještě řeč níže, nyní se podívejme na vzorec pro vážený průměr.
Vzorec pro vážený průměr
![]()
kde xi jsou jednotlivé hodnoty a wi jsou váhy (počáteční písmeno z anglického weight). Když už mluvíme o angličtině, průměr se řekne jako average nebo mean (ve smyslu střední hodnota), vážený průměr je weighted average.
Příklad
Vraťme se k našemu příkladu – testu ze statistiky –, kde jsme tvrdili, že výpočet průměru se zatříděnými hodnotami (do tabulky četností) je jen jiná forma váženého průměru. Všechny údaje uvádí následující tabulka. Váhami (wi) je počet studentů, kteří dostali danou známku (xi), jinými slovy četnosti známky neboli kolikrát se objevily.
| Známka xi | Počet studentů wi | Váženo xiwi | Vážený průměr |
|---|---|---|---|
| 1 | 3 | 3 | - |
| 2 | 6 | 12 | - |
| 3 | 7 | 21 | - |
| 4 | 2 | 8 | - |
| 5 | 2 | 10 | - |
| Suma | 20 | 54 | 54 ÷ 20 = 2,7 |
Jednotlivé známky odvážíme, tj. vynásobíme, počtem studentů (xiwi), vše sečteme a vydělíme sumou vah (wi). Výpočty jsou patrné z tabulky. Dospěli jsme k naprosto stejnému závěru, průměrná známka z testu ze statistiky je 2,7.
Tento příklad bychom mohli vypočítat ještě jedním způsobem. A to tak, že počty studentů, kteří dostali určitou známku (absolutní četnosti známek) bychom vyjádřili jako relativní četnosti, tj. jako podíly z celkového počtu. Například jedničku dostali 3 studenti z 20, relativní četnost (relativní váha) je 3/20 = 0,15. Dvojku dostalo 6 studentů z 20, tj. 6/20 = 0,3 atd. – viz následující tabulka, která zachycuje všechny výpočty.
| Známka xi | Počet studentů (absolutní četnost) | Váha (relativní četnost) wi | Vážený průměr xiwi |
|---|---|---|---|
| 1 | 3 | 3/20 = 0,15 | 1 × 0,15 = 0,15 |
| 2 | 6 | 6/20 = 0,30 | 2 × 0,30 = 0,60 |
| 3 | 7 | 7/20 = 0,35 | 3 × 0,35 = 1,05 |
| 4 | 2 | 2/20 = 0,10 | 4 × 0,10 = 0,40 |
| 5 | 2 | 2/20 = 0,10 | 5 × 0,10 = 0,50 |
| Suma | 20 | 1 | 2,7 |
Všimli jste si něčeho? Použijeme-li relativní četnosti jako váhy, pak jejich suma je rovna jedné. V tom případě nám odpadá jmenovatel vzorce pro vážený průměr (suma vah je jedna a jedničkou není třeba dělit, neboť dostaneme tu samou hodnotu). Hodnoty xi můžeme vynásobit vahami wi, sečíst a hned získat vážený průměr.
Stejně to funguje s pravděpodobností, neboť součet pravděpodobností se musí rovnat jedné. Z přísně matematického hlediska se pravděpodobnost uvádí jako desetinné číslo (nabývá hodnot 0 až 1), například pravděpodobnost, že hodíte mincí pannu, nebo orla, je 1/2 = 0,5. V praxi ale bývá často zvykem ještě vynásobit 100, aby hodnota byla v procentech (0,5 = 50 %).
Asi nejjednodušší případ použití pravděpodobnosti jako vah pro vážený průměr je jakákoliv sázka, kde máte pouze dva možné výsledky: výhru a prohru. Například vsadíte-li na červenou v ruletě, můžete vyhrát s pravděpodobností 18/37 a prohrát s pravděpodobností 19/37. Vynásobíte-li (vážíte-li) pravděpodobnost výhry tím, co můžete vyhrát, a pravděpodobnost prohry tím, co můžete prohrát (ztrátu vkladu – se záporným znaménkem), po sečtení získáte vážený průměrný výdělek, kdykoliv si tuto sázku podáte.
Na tom je dobré, že tento očekávaný vážený průměrný výsledek můžete použít i jako odhad do budoucna. Příklady najdete na stránce očekávaná hodnota, u všech loterijních her (tam může být i větší počet výsledků než dva – několik výherních pořadí vs. ztráta vkladu). Vážený průměr, kde jsou jako váhy pravděpodobnosti, lze využít ale i v podnikání a při investování.
Geometrický průměr
Geometrický průměr není tak často využívaný jako aritmetický průměr, najde ale uplatnění a podává věrohodnější výsledky u tzv. přírůstkových či růstových veličin. Ty se často používají v národohospodářství, například potřebujeme zjistit průměrné tempo růstu hrubého domácího produktu (HPD) nebo cen za posledních 5 let. Uveďme si nejprve vzorce (resp. vzorec, neboť oba vyjadřují totéž), k tomu malý komentář a samozřejmě příklad.
Vzorec pro geometrický průměr
![]()
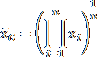
Geometrický průměr se vypočítá tak, že se všechny hodnoty (jejichž počet je n) mezi sebou vynásobí a z výsledného součinu se udělá n-tá odmocnina – viz první vzorec. Podmínkou je, že hodnoty jsou nezáporné (odmocnina ze záporného čísla není definována). Druhý vzorec pro geometrický průměr vyjadřuje naprosto totéž, je to jen zkrácený zápis. Velké řecké písmeno Π (pí) se používá pro součin všech hodnot, podobně jako se velká ∑ (sigma) používá pro součet všech hodnot. A pokud něco umocníme na (1/n), tak je to stejné jako provést n-tou odmocninu.
Příklad
Řekněme, že hrubý domácí produkt (HDP) nějaké země v posledních pěti letech rostl (jednou záporně, tj. poklesl) následovně: 4 %, 3 %, 1 %, -2 %, 1 %. Jaký je průměrný růst HDP?
Řešení:
Na úvod malá úvaha, co vůbec znamená růst (pokles). Například vezmeme-li loňský rok jako základnu (tj. 100 %) a vzrosteme-li o 4 %, jsme na 104 % minulého roku (104 % = 1,04). Pokud i příští rok znovu porosteme (tentokrát o 3 %), pak růst se počítá ze zvýšeného základu, tedy 1,04 × 1,03 atd. Dojde-li někdy v budoucnu k poklesu, například o 2 %, tak budeme na 98 % (0,98) předchozího roku. Tím dodržíme i požadavek, aby hodnoty byly nezáporné.
Můžeme proto spočítat, že oproti výchozímu roku HDP vzrostlo na úroveň:1,04 × 1,03 × 1,01 × 0,98 × 1,01 = 1,0709 či 107,09 %. Odečteme-li nyní jedničku (či 100 %), jakožto základ (výchozí stav), můžeme říci, že HDP vzrostlo o 7,09 procenta za 5 let.
A průměrný roční růst HDP na základě geometrického průměru určíme jakopátou odmocninu z 1,0709 = 1,0138 = 101,38 %, a tedy 1,38 % (po odečtení jedničky, resp. sta procent).
Poznámka: (1) výpočty jsou prováděny pomocí Excelu a nejsou zaokrouhlovány, (2) pátá odmocnina z nějakého čísla je totéž jako toto číslo na jednu pětinu (1/5). Například v Excelu se mocnina zadává jako „stříška“ (^), tak můžete zkusit do buňky vložit vzorec =1,0709^(1/5) a získáte přibližný výsledek 1,0138.
Odpověď:
Hrubý domácí produkt dané země rostl průměrným ročním (anualizovaným) tempem 1,38 procenta.
Ověřit bychom to mohli takto:
musí platit, že 1,04 × 1,03 × 1,01 × 0,98 × 1,01 = 1,01385 neboli (rozepsáno)
1,04 × 1,03 × 1,01 × 0,98 × 1,01 = 1,0138 × 1,0138 × 1,0138 × 1,0138 × 1,0138
(skutečné pohyby HDP v jednotlivých letech odpovídají tomu, jakoby HDP rostlo konstantním tempem 1,38 procenta ročně).
Počítat aritmetický průměr z procentuálních hodnot by nebylo natolik přesné, právě proto, že procentuální růsty se vztahují k různým základům. Dospěli bychom k výsledku:
4 % + 3 % + 1 % – 2 % + 1 % = 7 % ÷ 5 lety = 1,4 %.
V tomto případě se vypočtený aritmetický průměr (1,4 %) příliš neliší od geometrického průměru (1,38 %), ale v jiných případech by mohl být rozdíl větší a aritmetický průměr by mohl skutečné výsledky zkreslovat. Je možné zde uvést jednu vlastnost: geometrický průměr je vždy menší než nebo roven aritmetickému průměru.
Harmonický průměr
Harmonický průměr je ještě méně známou formou průměru. Začněme tím, jak je definován a vzorci. Harmonický průměr kladných čísel x1, x2 … xn je převrácená hodnota aritmetického průměru převrácených hodnot – viz následující vzorec.
Vzorec pro harmonický průměr
![]()
Dá se použít ještě jiná definice a zkrácený vzorec, které však znamenají totéž, a proto i samozřejmě vedou ke stejným výsledkům. Harmonický průměr je podíl rozsahu souboru a součtu převrácených hodnot statistických znaků:
![]()
Harmonický průměr lze využít tam, kde má smysl pracovat se součty převrácených hodnot (tj. jedna lomeno …). V praxi se využívá k zjištění průměrné délky času nutné k provedení nějakého úkonu, kdy jsou dané úkoly prováděny současně několika osobami či stroji apod. – viz následující příklad.
Příklad
V kavárně jsou provozovány dva kávovary současně. Příprava kávy na starším stroji zabere 3 minuty, zatímco na novějším stroji pouze 1,5 minuty. Jak dlouho trvá v průměru příprava jednoho šálku kávy?
Řešení:
Můžeme jednoduše dosadit třeba do druhého vzorce pro harmonický průměr:
2 ÷ (1/3 + 1/1,5) = 2 ÷ 1 = 2 minuty.
Ke stejnému výsledku se dostaneme i následující úvahou. Starší kávovar za hodinu vyrobí 20 šálků kávy (60 / 3), nový kávovar 40 šálků kávy (60 / 1,5). Průměrně tedy vyrobí (20 + 40) / 2 = 30 šálků kávy za hodinu (nyní jsme již mohli provést prostý aritmetický průměr, protože počty šálků kávy máme za stejný časový úsek 1 hodinu), to znamená 1 šálek kávy za 2 minuty.
Odpověď:
Průměrná délka času na přípravu jednoho šálku kávy je 2 minuty.
Naopak, kdybychom jednoduše spočetli aritmetický průměr jako (3 min + 1,5 min) / 2, získali bychom hodnotu 1 šálek kávy za 2,25 minuty, což je nesprávné.
Mohlo by vás také zajímat
- Statistika – úvod, základy;
- Absolutní a relativní četnost → histogram, polygon četností;
- Ukazatelé polohy a variability: modus a medián, rozptyl;
- Angličtina ve statistice;
- Průměrný roční (anualizovaný) výnos investice nebo z hraní pokeru;
- Průměrný hodinový výdělek – výpočet z měsíční mzdy pomocí koeficientu.
