Vyváženost kola rulety

Jak zjistíte nebo si přímo sami otestujete, zda je roztáčené malé kolo rulety vyvážené, či nikoliv? Kdy je častější či méně časté padání určitého čísla ještě normální z pohledu pravděpodobnosti, a kdy už ne? Vysvětlíme si postup na příkladu a vypočteme kritické hodnoty pro různé počty zatočení rulety.

Co je (ne)vyváženost ruletového kola

Co je vůbec vyváženost, či nevyváženost malého kola rulety? Odpověď už jsme trochu naznačili v úvodu. Malé kolo ve francouzské ruletě, která je pro hráče příznivější, má celkem 37 čísel (nezapomínejme na nulu). Každé jednotlivé číslo má naprosto stejnou pravděpodobnost, že bude vytočeno, a to přesně 1/37 – tedy za předpokladu, že kolo rulety je dokonale vyvážené.

Provedeme-li velký počet roztočení rulety (z angličtiny spinů), pak teoretická četnost výskytu každého čísla by měla být plus minus stejná či podobná. Skutečné četnosti se od teoretických mohou lišit a pomocí pravděpodobnosti a statistiky můžeme určit, zda je to ještě normální, či nikoliv.

Jak by takové testování kola rulety probíhalo

Buď data již máte k dispozici, například posledních 10 tisíc spinů, nebo vytočená čísla trpělivě zapisujete či jinak sledujete. Samozřejmě čím delší řada, tím lépe, tím věrohodněji pak mohou působit případné anomálie. Zjistíte, které číslo kolikrát padlo, jinak řečeno, jakou mělo četnost. Součet četností musí logicky dát celkový počet spinů.

Je nutné testovat každé jednotlivé číslo v ruletě zvlášť? Nikoliv. Vybereme si jen dvě čísla, která padla nejméně- a nejvícekrát. Potom jde o to, zda nejmenší či největší počet výskytů určitého čísla překročily kritickou dolní či horní mez, či nikoliv. Pokud nebyly kritické hodnoty překročeny, kolo rulety je možné považovat za vyvážené, a naopak. Tento postup se v matematické statistice nazývá testování hypotéz a něco si o něm také řekneme na konci stránky.

Nejprve si ale ukážeme jiný, snad snazší a pro laiky pochopitelnější postup (který prakticky znamená naprosto totéž), který už jsme na našem webu používali. Rovnou určíme interval pro přípustný počet výskytů určitého čísla. Jinak řečeno, pokud se četnosti jednotlivých čísel nacházejí v tomto intervalu, kolo je možné považovat za vyvážené.

Příklad – kdy je počet výskytů čísla OK, a kdy ne

Ruletu roztočíme celkem 3700×. Proč zrovna takové nekulaté číslo? Protože čísel je 37 a hned by nás mohlo napadnout, že každé číslo by teoreticky mělo být vytočeno 100×. To je kulaté číslo, které se dobře pamatuje a s kterým se dobře pracuje. K tomuto číslu se dostaneme nejen touto jednoduchou úvahou, ale i pomocí vzorce.

Pravděpodobnost v ruletě má tzv. binomické rozdělení (doporučujeme nezaleknout se názvu a stránku si projít), které představuje počet úspěchů (přičemž úspěch může nastat s pravděpodobností p) v n nezávislých pokusech. Přeloženo: jedno číslo v ruletě může padnout s pravděpodobností p = 1/37, počet úspěchů je, kolikrát toto číslo padne, a počet pokusů je celkový počet spinů n = 3700.

Střední hodnota (binomického rozdělení) se určí podle vztahu EX = np, v našem příkladu tedy EX = 3700 × 1/37 = 100. Střední hodnota představuje teoretický či očekávaný (Expected) počet výskytů jednoho čísla. Vidíme, že jsme se dostali ke stejnému závěru.

Nyní použijeme statistiku zvanou rozptyl, označíme ji zkratkou VAR (z angl. Variance). Ta určuje, jak mohou být skutečné počty spinů rozptýleny okolo střední očekávané hodnoty. Rozptyl u binomického rozdělení spočítáme podle vzorce VAR = np(1 – p), (celkový počet spinů krát úspěch krát neúspěch, který je navíc zohledněn), v našem příkladu VAR = 3700 × 1/37 × 36/37 = 97.

Z rozptylu spočítáme tzv. směrodatnou odchylku, označíme ji SD (Standard Deviation). Směrodatná odchylka je vždy druhá odmocnina z rozptylu (nevíte-li proč, prohlédněte si stránku o rozptylu a směrodatné odchylce), SD = 10. Všechny výpočty jsou prováděny pomocí Excelu bez zaokrouhlování, čísla za desetinnou čárkou pouze nejsou zobrazena.

Konečně použijeme pravidlo o třech směrodatných odchylkách (pravidlo 3-SIGMA) pro vymezení intervalů, resp. pro nízké a vysoké počty výskytů čísla, které jsou ještě OK. Pravidlo říká, že asi 95 procent hodnot se nachází do vzdálenosti plus minus 2 směrodatné odchylky od střední hodnoty, a něco více než 99 procent všech hodnot ve vzdálenosti plus minus 3 směrodatné odchylky.

Zrekapitulujme: EX = 100, SD = 10.

Pro 95% interval platí:

dolní mez = EX – 2 × SD = 100 – 2 × 10 = 80,
horní mez = EX + 2 × SD = 100 + 2 × 10 = 120.

Resumé? Roztočíme-li ruletu 3700krát, pak četnost každého čísla by se měla pohybovat okolo 100 spinů (střední hodnota). Padne-li nějaké číslo méně než 80× nebo více než 120×, pak na 95 % je kolo rulety nevyvážené. Respektive, existuje pouze 5procentní pravděpodobnost, že by kolo bylo vyvážené.

Pro 99% interval platí:

dolní mez = EX – 3 × SD = 100 – 3 × 10 = 70,
horní mez = EX + 3 × SD = 100 + 3 × 10 = 130.

Resumé? Úvod je stejný jako v předchozím resumé… A dále, padne-li nějaké číslo méně než 70× nebo více než 130×, pak na více než 99 % je kolo rulety nevyvážené. Respektive, existuje pouze méně než 1procentní pravděpodobnost, že kolo je vyvážené.

Pokud byste měli pocit, že kulička zapadá do určitého místa na kole rulety častěji, můžete vyzkoušet sázku na sousední čísla. Dal by se také otestovat určitý úsek ruletového kola.

Kritické hodnoty pro různé počty spinů

Výpočty pro různé počty spinů, směřující k rozhodnutí, zda je kolo rulety vyvážené s pravděpodobností 95 a 99 procent, jsou uvedeny v Tabulce 1. Kritické hodnoty pro nejnižší a nejvyšší počet padnutí jakéhokoliv čísla jsou šedě podbarveny.

Tabulka 1: Vyváženost kola rulety – kritické hranice pro různé počty spinů

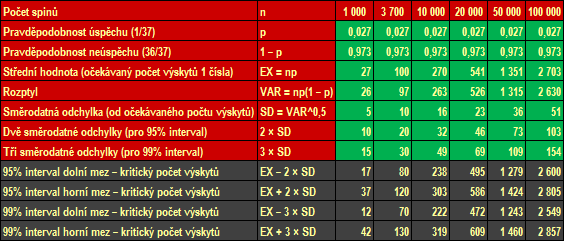
Například provedete-li 10 000 roztočení rulety (spinů) nebo máte-li již vzorek těchto dat, pak by žádné číslo nemělo padnout méně než 238× a více než 303×, aby bylo možné kolo rulety s pravděpodobností 95 % považovat za vyvážené.

U pravděpodobnosti 99 % je interval, kdy je kolo možné považovat za vyvážené, širší, a to 222 až 319. Pokud by nějaké číslo bylo vytočeno méněkrát nebo vícekrát než tyto hranice, pak hypotézu o vyváženosti kola zamítáme (existovala by pouze 1procentní šance, že kolo je vyvážené).

Využití v praxi? Pokud na dostatečně velkém počtu spinů odpozorujete, že některé číslo padá vícekrát než by odpovídalo teoretickému předpokladu (jestliže některé číslo padá málokrát, tak vám to stejně nebude moc k užitku), tj. počet výskytů čísla by byl vyšší než je horní kritická mez, pak by asi stálo začít na toto číslo opakovaně sázet a skutečně v ruletě vyhrávat. Mimochodem, víte, která sázka v ruletě je statisticky nejlepší? Provedli jsme také řadu testů ruletových sázek i systémů sázení. Můžete se podívat, jak dopadl test sázky na jedno číslo.

Testování hypotézy, že kolo rulety je vyvážené

Testování hypotéz je matematický „terminus technikus“, občas se proto nevyhneme matematickým pojmům, ale vše snad „lidsky“ upřesníme.

Naměříme nějaký vzorek dat, tj. třeba 3700 spinů. Víme, které číslo kolikrát padlo, tj. jakou mělo četnost. Ruleta má 37 čísel, každé číslo by teoreticky mělo padat s pravděpodobností 1/37. Při 3700 spinech to dělá 100 výskytů (četnost 100) pro každé číslo.

Vybereme si číslo s nejmenší a největší četností. Testujeme hypotézu, že kolo je vyvážené, resp. přesněji testujeme hypotézu, že číslo s nejmenší a největší četností padá s pravděpodobností 1/37 proti alternativní hypotéze, že nepadá s pravděpodobností 1/37. Padá = kolo je vyvážené, nepadá = kolo je nevyvážené.

Ještě předtím si zvolíme tzv. hladinu významnosti, označovanou řeckým písmenem alfa, obvykle volíme 5 % nebo 1 %, tzn., že kritickou oblast tvoří 5 % resp. 1 % hodnot (stejná logika jako u intervalů výše). Vypočítáme kritické hodnoty pro nejmenší a největší počet padnutí čísla.

Pokud si zvolíme hladinu významnosti 5 %, pak 95 % hodnot rozprostřených rovnoměrně okolo střední očekávané hodnoty považujeme za přípustné (kolo je vyvážené). Zleva (malý počet padnutí čísla) i zprava (velký počet padnutí čísla) zbývá po 2,5 procentech. To jsou oblasti kritických hodnot – příliš malý nebo příliš velký počet padnutí určitého čísla, kdy hypotézu o vyváženosti ruletového kola zamítáme. Existuje jenom 5procentní šance, že bychom zamítli hypotézu, která je správná, tzn., že existuje pouze 5procentní šance, že by kolo rulety bylo opravdu vyvážené.

Na dále uvedené výpočty existují funkce, třeba v Excelu. Nicméně kdybychom otrocky chtěli spočítat oblast kritických hodnot zleva (malých hodnot), tak bychom spočítali pravděpodobnost, že jedno číslo ze 3700 spinů nepadne vůbec, padne právě 1×, právě 2× až právě k-krát → návod, vzorce, vysvětlení a příklady viz binomické rozdělení. Tyto pravděpodobnosti bychom sčítali (kumulovali), až bychom se dostali co nejblíže součtu 0,025 (tj. 2,5 % – viz výše). „Ká“, u kterého bychom se zastavili, je kritická dolní hranice, zde k = 79, protože k = 80 je již přípustné.

Obdobně bychom postupovali zprava a počítali pravděpodobnost, že nějaké číslo padne právě 3700× z 3700 spinů, právě 3609× atd. Pravděpodobnosti takto malých a velkých počtů padnutí jednoho čísla jsou ovšem velmi nízké a rostou směrem ke střední hodnotě.

Mohlo by vás také zajímat

• Zaručený výdělek v ruletě?
• Jak by šlo na ruletě opravdu vydělat;
• Články o pravděpodobnosti a statistice;
• Deziluze hráče rulety – jásat, když dlouho nešla jedna barva?
• Kolik zatočení rulety stačí k tomu, abyste s téměř jistotou začali prodělávat;
• Nejlepší sázka v ruletě;
• Ruletní systémy;
• Testy ruletních systémů a sázek.