Hazardní hry › Pravděpodobnost › Binomické rozdělení

Binomické rozdělení – počet úspěchů při opakování pokusu

I když nejste zrovna kovaní v matematice, nemusíte se zalekat názvu této stránky. Dozvíte se například, jakým způsobem si můžete spočítat pravděpodobnost toho, že v deseti hodech kostkou hodíte šestku třeba právě třikrát nebo minimálně třikrát apod.

Teoretické minimum

Než se pustíme do příkladu, na kterém si vše vysvětlíme, uveďme si trošku nezbytné teorie a velmi užitečný vzorec.

Řečeno jazykem matematiky, binomické rozdělení Bi(n, p) představuje počet úspěchů k v n nezávislých pokusech, přičemž pravděpodobnost úspěchu p je 0 < p < 1. Dodejme, že binomické rozdělení se v literatuře též označuje jako Bernoulliho schéma. Pravděpodobnost, že úspěch nastane právě k-krát z n pokusů při pravděpodobnosti úspěchu p, je určena (binomickým) rozdělením:

Poznámka: binomické rozdělení je součet n nezávislých alternativních rozdělení, které představuje pouze jeden pokus se dvěma možnými výsledky: úspěch/neúspěch.

Příklad

Držme se našeho příkladu s kostkou. Budeme házet obyčejnou šestihrannou kostkou 10× po sobě, jinak řečeno, provedeme deset pokusů (n = 10). Budeme se snažit hodit šestku (avšak stejný závěr by platil i pro ostatní čísla). Předem můžeme spočítat pravděpodobnost, že šestku nehodíme vůbec, tj. nulakrát (k = 0), že šestku hodíme právě jedenkrát (k = 1), právě dvakrát (k = 2) až právě desetkrát (k = 10).

Pravděpodobnost, že hodíme šestku, jinými slovy, pravděpodobnost úspěchu, je v každém hodu 1/6 (p = 1/6). Výraz (1 – p) ve vzorci je pravděpodobnost neúspěchu. Možnosti jsou jen dvě: úspěch, nebo neúspěch. Pravděpodobnost neúspěchu je doplněk do jedné (či sta procent, pokud bychom pravděpodobnost vyjadřovali v procentech), tedy 1 – 1/6 = 5/6.

V úvodu jsme uvedli, že si budete schopni spočítat například pravděpodobnost, že z deseti hodů kostkou hodíte šestku právě třikrát. Slovo právě znamená, že v tomto případě šestku hodíme přesně třikrát z deseti pokusů, nikoliv méněkrát, ani vícekrát. Jednoduše dosadíme do vzorce uvedeného výše:

Pravděpodobnost, že z deseti hodů kostkou hodíme šestku právě třikrát, je 0,155 či 15,5 %.

Vysvětlení vzorce a výpočtů

Vzorec a výpočty si zasluhují komentář. Výraz , zde konkrétně , je tzv. kombinační číslo, které čteme „n nad k“, resp. „deset nad třemi“, a jenž představuje počet kombinací. To dále násobíme pravděpodobností úspěchu umocněnou na požadovaný počet úspěchů (3, tj. na třetí) a dále násobíme pravděpodobností neúspěchu umocněnou na zbytek do desíti (7, tj. na sedmou).

Proč umocňování? Pravděpodobnosti na sebe navazujících událostí se násobí. Pokud bychom například házeli jen třikrát a ptali se na pravděpodobnost, že třikrát po sobě hodíme šestku, mohli bychom výpočet zkrátit takto: 1/6 × 1/6 × 1/6 = (1/6)³ = 0,00463 = 0,463 % (neúspěch by byl na nultou, to je jedna, a kombinace tři nad třemi je rovněž jedna, proto je můžeme ze vzorce vynechat).

Proč jsou ve vzorci kombinace? Házení kostkou desetkrát po sobě a sledování čísel, která padnou, si také můžeme představit tak, že vezmeme do hrsti deset kostek najednou a pustíme je na zem. Tři šestky v tomto příkladu se mohou objevit na jakékoliv z deseti kostek. Proto musíme spočítat všechny možné kombinace, kterých je „deset nad třemi“, což dává 120 různých kombinací! Viz následující ilustrace, kde se šestka objevila na 3 kostkách z 10; je to jen jedna ze 120 možných kombinací:

Pravděpodobnost dosažení právě „ká“ úspěchů

K výpočtu pravděpodobnosti, že šestku hodíme právě třikrát z deseti hodů, můžeme použít třeba Excel. Po zadání vzorce =KOMBINACE(10;3)*(1/6)^3*(5/6)^7 obdržíme výše zmíněný (zaokrouhlený) výsledek 0,155 či 15,5 %.

Pravděpodobnosti pro všechny počty úspěchů nula- až desetkrát jsou spočteny v Tabulce 1 – viz sloupec Pravděpodobnost právě k [ká] úspěchů. Označovat hození šestky nulakrát (vůbec) jako úspěch zní trochu paradoxně, ale úspěchem je zde míněno, že se šestku podaří hodit právě nulakrát.

Můžeme vidět, že při deseti hodech kostkou je nejpravděpodobnější výsledek, že se nám šestku podaří hodit pouze jednou: vzorec v Excelu by vypadal takto =KOMBINACE(10;1)*(1/6)^1*(5/6)^9 a dal výsledek 0,323 = 32,3 %.

Naopak pravděpodobnost, že by se nám šestku podařilo hodit desetkrát po sobě (pokaždé), je naprosto mizivá: =KOMBINACE(10;10)*(1/6)^10*(5/6)^0. Vzorec by šlo opět zkrátit, protože kombinace stejných čísel nad sebou je jedna a pět šestin na nultou, jakožto cokoliv na nultou (kromě nuly na nultou, což je neurčitý výraz), je také jedna. Zkrácený vzorec v Excelu vypadá takto =(1/6)^10 a dává výsledek uvedený v Tabulce 1.

Lépe uchopitelný tento výsledek bude, pokud jej převedeme na pravděpodobnost ve formátu sázkového kurzu (1 ku …), tj. provedeme jeho převrácenou hodnotu (1 děleno pravděpodobnost) a získáme hodnotu 60 466 176. Pravděpodobnost, že bychom 10× po sobě hodili šestku, je pouze 1 ku zhruba 60 milionům!

Tabulka 1: Pravděpodobnost při 10 hodech kostkou (matematický – desetinný formát)

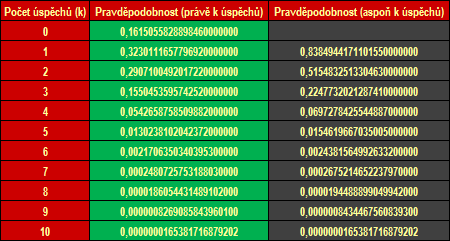
Pravděpodobnost při deseti hodech kostkou

V striktně matematickém pojetí pravděpodobnost dosahuje hodnot 0 (jev nemožný) až 1 (jev jistý). Proto někteří matikáři neradi vidí pravděpodobnost v procentech. Tabulka 2 zachycuje naprosto stejné výsledky jako Tabulka 1, avšak pravděpodobnosti jsou převedeny do formátu sázkového kurzu, tj. 1 ku výsledek v tabulce.

Tabulka 2: Pravděpodobnost při 10 hodech kostkou jako sázkový kurz (1 ku …)

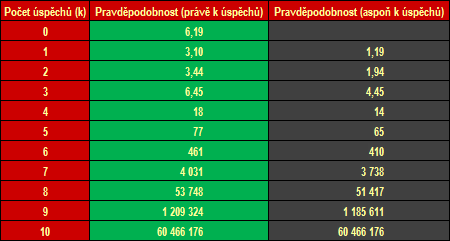
Pravděpodobnost při deseti hodech kostkou ve formátu 1 ku

Pravděpodobnost, že dosáhneme alespoň „ká“ úspěchů

Například, co znamená, že z deseti hodů kostkou hodíme alespoň 1krát šestku? To znamená, že ji hodíme jedenkrát nebo dvakrát nebo … nebo až desetkrát. Pravděpodobnost, že alespoň 1krát hodíme šestku z deseti hodů, pak spočítáme tak, že sečteme pravděpodobnosti toho, že šestku hodíme právě jedenkrát, právě dvakrát až právě desetkrát – viz druhý řádek ve třetím sloupci Tabulky 1 a získáme hodnotu přibližně 0,8385 = 83,85 %. Pravděpodobnost, že hodíme šestku právě dvakrát a vícekrát logicky postupně klesá.

Dále můžeme s výhodou využít doplňku pravděpodobnosti (do jedné, neboť součet pravděpodobností musí být vždy roven jedné).

Například pravděpodobnost, že nehodíme šestku vůbec (nulakrát), můžeme spočítat buď přímo dosazením do vzorce výše (v Excelu =KOMBINACE(10;0)*(1/6)^0*(5/6)^10, tj. 0 úspěchů, 10 neúspěchů; vzorec by šlo i zkrátit =(5/6)^10) nebo pomocí doplňku.

Protože známe-li pravděpodobnost, že hodíme šestku 1× až 10×, doplňkem do jedné je pravděpodobnost, že šestku nehodíme vůbec. Známe-li například pravděpodobnost, že šestku nehodíme vůbec nebo jen jedenkrát, tak doplňkem je, že šestku hodíme 2× až 10× (tj. alespoň dvakrát) apod.

→ Další příklad? Binomické rozdělení bylo prakticky použito již v roce 1710 jako „důkaz o božské prozřetelnosti!“ nebo Házení mincí – sázky a pravděpodobnost.

Střední hodnota a rozptyl u binomického rozdělení

Zase to zní trochu moc matematicky, ale opět vysvětlíme na příkladu, o co jde. Nejprve si uveďme vzorce a pokračujme pod nimi. Dodejme, že střední hodnota a rozptyl jsou užitečné charakteristiky jakéhokoliv souboru dat (například výsledky několika hodů kostkou atd.).

Střední hodnotu u binomického rozdělení vypočítáme podle vzorce:

Rozptyl u binomického rozdělení určíme podle vzorce:

Poznámka, souvislost: vzorce jsou stejné jako u alternativního rozdělení (kde je 1 pokus, jehož výsledkem je úspěch/neúspěch), avšak jsou vynásobeny n, tj. počtem pokusů.

Praktické využití – příklad

Předpokládejme, že bychom provedli 600 hodů kostkou (n = 600). Pravděpodobnost, že padne šestka v jednom hodu, je p = 1/6. Něco nám napovídá, že teoreticky by každé číslo (tedy i šestka) mělo padnout 100krát (6 čísel × 100 četností výskytu = 600 hodů).

Střední hodnota je určitý očekávaný, teoretický výsledek, ke kterému by provádění pokusu (házení kostkou) mělo směřovat, a to tím spíše, čím déle budeme kostkou házet. U binomického rozdělení můžeme střední hodnotu spočítat přesně, v jiných případech v praxi je třeba ji někdy odhadnout pomocí aritmetického průměru nebo modu či mediánu. Zůstaneme-li u šestky (platí to však pro všechna čísla), pak střední hodnota po dosazení do vzorce je:

E(X) = np = 600 × 1/6 = 100.

Šestka by teoreticky měla (ale rozhodně nemusí) padnout 100krát. Rozptyl ukazuje, jak moc se může skutečnost lišit od tohoto teoretického předpokladu:

Var(X) = 600 × 1/6 × (1 – 1/6) = 83,33.

Tzv. směrodatná odchylka je druhá odmocnina z rozptylu, což je asi 9.

Pravidlo 3-SIGMA pak mj. říká, že asi 95 % hodnot leží ve vzdálenosti plus minus dvě směrodatné odchylky od střední hodnoty, zde tedy 100 – 2 × 9 a 100 + 2 × 9, tzn. v intervalu 82 až 118. Tři směrodatné odchylky pokrývají více než 99 % hodnot.

Jak můžeme tuto znalost v praxi využít? Pokud by některé číslo padlo méně než 82× nebo více než 118× z 600 hodů, mohli bychom vážně pochybovat o tom, že kostka je dobře vyvážená. Jinak řečeno, existovala by jen 5procentní pravděpodobnost, že kostka je dobře vyvážená.

Testovali jsme také ruletové kolo, zda je vyvážené, a vymezili kritické hranice pro různé počty zatočení rulety. Můžete si také přečíst návod, jak by se vyššího výskytu určitých čísel v ruletě dalo využít a vydělat na tom. Další vysvětlující informace a názorné příklady naleznete pod odkazy v této kapitole.

Mohlo by vás také zajímat

Sdílej tuto stránku na Facebooku