Výpočet variance u SnG pro 9 hráčů
Dnes provedeme výpočet variance zaměřený přímo na poker, konkrétně na miniturnaj typu Sit and Go (SnG) pro 9 hráčů. Ukážeme si, jak zjistíme výdělek, který můžeme očekávat v jednom SnG turnaji. Dále, jakou při tom máme varianci, tj., jak se mohou skutečné výdělky – například po odehrání 1000 SnG – lišit od očekávaných. To nám pomůže odpovědět třeba na otázku „Jaký počet turnajů SnG musím odehrát, abych s pravděpodobností více než 99 % zůstal minimálně na svém?“ Nepostradatelná pomůcka pro hráče, kteří to s pokerem myslí vážně.
Základy
Jestliže je téma „Variance v pokeru“ pro vás nové, zkuste se nejprve podívat na naše dříve publikované články:
- Co je variance a hodnota $ EV Adjusted?
Naleznete zde základní popis variance, jakou roli může hrát náhoda a jak se dá spočítat, zdali jste měli v určitém herním období štěstí, nebo smůlu. - Význam a výpočet variance krok po kroku.
Na jednoduchém příkladu dvou her s mincí je podrobně vysvětlen výpočet variance, její význam a praktický dopad na hru. Stačí papír, tužka, kalkulačka a ověřit si, že to není až tak složité, jak se může na první pohled zdát. Výpočty variance pro poker jsou naprosto stejné a vychází z nich i dnešní příklad na miniturnaj Sit and Go pro 9 hráčů.
Sit and Go pro 9 hráčů – příklad
V dnešním příkladu budeme hrát turnaj SnG pro 9 hráčů. Buy-in je $5+0,5. Placena jsou první tři místa v poměru 50/30/20. Cenový fond (prize pool) tedy činí 9 hráčů × $5 = $45. Padesát centů je poplatek provozovateli hry (rake), který se do prize poolu nepočítá.
Za první místo hráč obdrží 50 % z $45, tedy $22,50. V čistém vyjádření, tj. po odečtení vkladu do hry $5, je to $17,50. Podobně postupujeme i u ostatních placených pozic. Přitom pro zjednodušení neodečítáme rake a nepočítáme také s možností vrácení raku (rake back) a různých bonusů, které hráč může za hru obdržet. Můžeme zrekapitulovat hrubé a čisté (v závorce) výdělky za umístění v turnaji:
1. místo: $22,50 ($17,50),
2. místo: $13,50 ($8,50),
3. místo: $9,00 ($4,00),
4. – 9. neplacená místa: $0,00 (-$5,00).
Jaký můžeme očekávat výdělek? Nejprve se podíváme do našich dlouhodobých statistik a zjistíme, jak často se dostáváme na placené pozice. Údaje mohou být uvedeny přímo v procentech, nebo v absolutním počtu. Například zjistíme, že z 10 000 her jsme skončili 1 300krát na prvním místě, tzn. v 13 procentech všech případů. Toto číslo považujeme za pravděpodobnost, s jakou i v dalších turnajích obsadíme první místo. Řekněme, že na (placené) pozice se dostaneme s těmito pravděpodobnostmi (= v těchto procentech případů):
1. místo: 13 %,
2. místo: 12 %,
3. místo: 10 %,
4. – 9. neplacená místa: 65 % (zbytek do 100 %).
Výpočet EV, VAR, SD
Získali jsme dva nezbytné údaje: (1) pravděpodobnosti umístění na placených a neplacených pozicích a (2) čisté výhry, které můžeme získat, a stejně tak bereme v úvahu, že můžeme i ztratit buy-in, pokud se neumístíme na placené pozici –, které nám stačí na to, abychom mohli provést všechny výpočty. To znamená výpočet:
- očekávaného výdělku (či zisku, i když teoreticky bychom mohli být dlouhodobě ztrátoví) na základě očekávané hodnoty (EV),
- variance (VAR) jako možného rozptylu hodnot od očekávaného výdělku a
- směrodatné odchylky (SD), která nám pomůže určit intervaly, v nichž se s určitou vysokou pravděpodobností budeme pohybovat (tím jsou myšleny naše skutečné výdělky).
Všechny vstupní údaje (pravděpodobnosti umístění a čisté výhry) a všechny výpočty uvádí přehledným způsobem Tabulka 1.
Tabulka 1: Výpočet EV, VAR a SD u pokerového miniturnaje SnG pro 9 hráčů
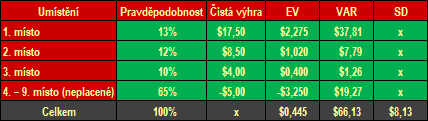
K hodnotám EV, VAR a SD jsme se dostali níže uvedeným způsobem. Je-li třeba či chcete-li jim lépe porozumět, navštivte prosím výše doporučenou stránku Variance – jednoduchý příklad, kde jsou všechny výpočty podrobně a srozumitelně okomentovány.
EV = 0,13 × $17,5 + 0,12 × $8,5 + 0,1 × $4 + 0,65 × (−$5) = $2,275 + $1,020 + $0,400 − $3,250 = $0,445.
Velmi stručně k výpočtu EV: pravděpodobnosti umístění (v desetinném tvaru, 13 % = 0,13 atd.) krát možné výhry z daného umístění minus pravděpodobnost prohry (neumístění se na placených pozicích) krát ztráta buy-inu.
Po jednom odehraném SnG turnaji pro 9 hráčů můžeme – na základě našich dlouhodobých výsledků – očekávat zisk přesně $0,445 (neboli 44,5 centu). To by indikovalo rentabilitu (zhodnocení) vložených prostředků, tzv. ROI = 8,09 % ($0,445 děleno buy-inem $5,5 krát 100 %).
VAR = 0,13 × ($17,5 − $0,445)2 + 0,12 × ($8,5 − $0,445)2 + 0,1 × ($4 − $0,445)2 + 0,65 × (−$5 − $0,445)2 = $66,13.
Variance ukazuje možný rozptyl hodnot (poznámka: český překlad anglického slova variance je právě rozptyl). Umocněním všech rozdílů jednotlivých výdělků od očekávaného získáme ze záporných hodnot kladné. Každý umocněný rozdíl je opět vážen pravděpodobností (ne)umístění. Nyní z variance získáme (směrodatnou) odchylku, která ukazuje jak moc do minusu a do plusu se skutečné výdělky mohou odlišovat od očekávaného výdělku (EV), a to tak, že varianci jednoduše odmocníme (druhá odmocnina):
SD = druhá odmocnina z $66,13 = $8,13.
Poznámka: výpočty jsou prováděny pomocí Excelu, který standardně počítá na 15 desetinných míst, zobrazeny jsou obvykle pouze 2.
Interval, v kterém se bude nacházet zisk s určitou pravděpodobností
Nyní platí statistické pravidlo o třech směrodatných odchylkách (3 SIGMA) – nad tím nemusíte přemýšlet, prostě to můžete brát jako fakt (praktický význam uvidíte níže) –, které říká, že:
- téměř 70 % hodnot (přesně 68,27 %) se nachází v intervalu
EV ∓ SD, - asi
95 %hodnot (přesně 95,45 %) leží v intervaluEV ∓ 2 × SD, - asi
99 %hodnot (přesně 99,73 %) leží v intervaluEV ∓ 3 × SD.
Jinak řečeno, přesně 68,27 % všech hodnot (míněno našich možných výdělků) se bude nacházet ve vzdálenosti minus plus jedna odchylka (SD) od očekávané střední hodnoty (EV); přesně 95,45 % všech možných výdělků se bude nacházet v intervalu minus plus dvě odchylky (2 SD); a přesně 99,73 % všech možných výdělků se bude nacházet v intervalu minus plus tři odchylky (3 SD).
Zajímat nás budou především poslední dva intervaly, zjednodušeně 95 % a 99 %, které se téměř blíží jistotě (100 %). Ještě dodatek: minus SD (ať už s jakýmkoliv násobkem) určuje dolní mez intervalu (min) a plus SD horní mez intervalu (max).
Jak na tom budeme třeba po 1000 SnG?
Nyní předpokládejme, že se rozhodneme, třeba za určité období, odehrát 1000 miniturnajů SnG pro maximálně 9 hráčů. Jak na tom budeme, resp. jak využijeme předchozí výpočty EV, VAR a SD?
Vyjdeme z jednoduchého předpokladu, že pokud v jednom SnG očekáváme průměrný zisk $0,445, pak po tisíci odehraných SnG můžeme očekávat zisk (EV) tisíckrát větší, tedy 1000 × $0,445 = $445. Rovněž variance (VAR) bude tisíckrát větší, tj. 1000 × $66,13 = $66 134 (připomínáme, že používáme výpočty bez zaokrouhlování). Pozor ale, směrodatná odchylka (SD) se vypočítá jako druhá odmocnina z variance (nebo jako jednotlivá SD krát odmocnina z počtu odehraných turnajů).
Pro 1000 SnG platí:
EV = 1000 × $0,445 = $445
VAR = 1000 × $66,13 = $66 134
SD = druhá odmocnina ze $66 134 = $257
Určeme dolní (min) a horní mez (max) intervalů 95 % a 99 %.
95 % (přesně 95,45 %):
min = EV − 2 × SD = $445 − 2 × $257 = −$69
max = EV + 2 × SD = $445 + 2 × $257 = +$959
Co z výpočtů vyplývá? Po tisíci odehraných SnG turnajích budu očekávat (průměrný) zisk $445. Skutečný zisk (či ztráta) se na 95,45 procenta bude pohybovat v intervalu −$69 až +$959. To lze říci i takto: po 1000 turnajích bych měl vydělat asi 445 dolarů, ale kdyby se mi neskutečně nedařilo, mohl bych dokonce skončit v minusu 69 dolarů (downswing). Na druhou stranu je možné, že kdybych měl mimořádné štěstí (upswing), tak mohou vydělat až 959 dolarů (obě hodnoty oproti předpokládaným +445 dolarům).
A ještě jednu věc můžeme konstatovat: přestože bychom měli v průměru vydělat asi 44,5 centů z každého odehraného SnG $5+0,5, tak 1000 turnajů s naší variancí není dostatečný počet k tomu, aby se to s 95procentní pravděpodobností potvrdilo. Při nejhorším možném scénáři můžeme prodělat 69 dolarů.
Můžeme si pak položit otázku, kolik je potřeba odehrát těchto turnajů, abychom alespoň neprodělali. To znamená, že hledáme takový počet turnajů n, kdy dolní mez intervalu (min) se rovná nule. Po úpravách získáme následující vzorec (v něm jsou hodnoty VAR a EV za jeden turnaj):
n = 4 × VAR ÷ EV2
Po dosazení n = 4 × $66,13 ÷ $0,4452 = přibližně 1336 turnajů.
Museli bychom odehrát asi 1336 SnG, abychom s asi 95procentní jistotou skončili při nejhorším možném průběhu na nule.
Nyní se podívejme, co se stane, pokud chceme zvýšit pravděpodobnost na více než 99%.
99 % (přesně 99,73 %):
min = EV − 3 × SD = $445 − 3 × $257 = −$326
max = EV + 3 × SD = $445 + 3 × $257 = +$1216
Se zvýšením pravděpodobnosti na více než 99 % se rovněž a pochopitelně rozšířil interval, v kterém se naše skutečné výsledky mohou s touto pravděpodobností nacházet. Oproti 95procentnímu intervalu se totiž berou tři odchylky (3 SD) do minusu a do plusu, namísto dvou odchylek (2 SD).
Při stejném očekávaném průměrném výdělku (ten se nemění) 445 dolarů z 1000 SnG, se s více než 99procentní pravděpodobností náš skutečný výdělek bude pohybovat v rozmezí −$326 až +$1216. Pokud bychom měli extrémní smůlu, mohli bychom prodělat až 326 dolarů, a to přesto, že hrajeme slušně (ROI = 8,09 %). To pravděpodobnost připouští. Na druhou stranu variance působí i opačným směrem a při mimořádném štěstí bychom mohli vydělat 1216 dolarů oproti předpokládaným 445 dolarům. Můžeme si znova položit následující otázku.
Kolik turnajů musím odehrát, abych na 99,73 % minimálně neprodělal?
Podmínka se stejná jako u intervalu 95 %, a sice že dolní mez intervalu (min) se musí rovnat nule. Zde však působí tři odchylky (3 SD), proto vzorec pro výpočet počtu turnajů n, při kterém se min = 0 je následující:
n = 9 × VAR ÷ EV2
Opět do vzorce dosaďme hodnoty VAR a EV za jeden turnaj SnG:
n = 9 × $66,13 ÷ $0,4452 = přibližně 3006 turnajů.
Museli bychom odehrát minimálně 3006 turnajů, abych s pravděpodobností převyšující 99 % (přesně 99,73 %) skončili minimálně na nule (lehce v plusu). Všimli jste si, že abychom zvýšili šanci, že neproděláme, o zhruba 4 procentní body (z 95,45 % na 99,73 %), tak bychom museli odehrát více než dvojnásobný počet turnajů?
Ještě to zkusme ověřit. Pro 3006 odehraných turnajů SnG platí:
EV = 3006 × $0,445 = $1338
VAR = 3006 × $66,13 = $198 800
SD = druhá odmocnina ze $198 800 = $446
Pořád se nacházíme v intervalu, který pokrývá 99,73 % všech možných výdělků (i ztráty):
min = EV − 3 × SD = $1338 − 3 × $446 = $0
max = EV + 3 × SD = $1338 + 3 × $446 = +$2676
Vidíme, že po 3006 odehraných turnajích bychom s pravděpodobností vyšší než 99 % měli vydělat $1338 (to je střední průměrný odhad výdělku), a že při nejhorším možném průběhu bychom skončili nejhůře na nule, tj. neprodělali.
Závěr
Příklad výpočtu variance u miniturnaje Sit and Go pro max. 9 hráčů ukázal její význam a praktické důsledky pro hru. I dobrý pokerový hráč – poker je především o dovednosti, nikoliv (jen) o náhodě – s dobrou strategií, která mu zajišťuje dlouhodobou kladnou rentabilitu (ROI), může zažít období, kdy nevydělá ani dolar nebo dokonce prodělá. Může za to variance, která měří velikost možných výkyvů od hráčova průměrného dlouhodobého výdělku (= ROI).
Pokerový hráč musí varianci přijmout jako fakt a být trpělivý. Je to nepříjemné, především když se nedaří. Avšak při dobré dlouhodobé strategii je variance potlačena – čím více her (turnajů) hráč odehraje, tím blíže se jeho výdělky budou pohybovat kolem dlouhodobého průměrné ziskovosti. Je žádoucí, aby hráč dosahoval co nejvyšší EV a co nejnižší VAR.
Jelikož variance působí oběma směry, může být i příjemná. Ukazuje také, kam až mohou vaše výdělky dosáhnout, pokud by se extrémně zadařilo. Nicméně v dlouhém období, tzn. po velkém počtu odehraných her/turnajů, se výdělky vrací k průměru.
Vyšší variance však zvyšuje nároky na bankroll management – s většími výkyvy musíte odehrát větší počet her a mít na to větší kapitál, abyste to utáhli a vaše (dobrá) strategie se nakonec projevila. Hráč, který chce mít stabilní výdělky, neřkuli se hraním pokeru živí, má rozhodně zájem na co nejnižší možné varianci.
Může se hodit / kam dál:
