Hazardní-Hry.eu
Hazardní hry › Karty › Poker › Variance – příklad

Variance – příklad

Jednoduchý a názorný příklad na výpočet variance dokresluje její praktický význam a využití. Spočítáme si dlouhodobý očekávaný výdělek (z provozování nějaké hry nebo z hraní pokeru) a varianci jako možné odchylky od očekávaného výdělku. Po přečtení budete například schopni odpovědět na otázku „Kolik musím odehrát her, abych na 99 procent neprodělal?“

Co je variance

Variance je statistika, která ukazuje, jak se krátkodobé výdělky hráče liší nebo mohou lišit od jeho dlouhodobého průměru. Čím více hand hráč odehraje, tím více se vykrystalizovává ziskovost, které je schopen v dlouhém období dosáhnout.

Pokerový hráč tedy může s určitou mírou pravděpodobnosti očekávat určitou ziskovost. Může nastat období, kdy má hráč smůlu a jeho ziskovost je nižší než očekávaná (= nižší než jeho dlouhodobý průměr). Tento fenomén je nazýván jako downswing. Hráč ovšem může mít i období, kdy se mu daří víc než obvykle (má štěstí) a dosahuje vyšší ziskovosti než je jeho dlouhodobý průměr. V tomto případě jde o tzv. upswing.

„Mantinely“, v kterých se hráč pohybuje, se právě nazývají variance (česky rozptyl, nicméně anglické slovo variance již zdomácnělo i mezi českými pokerovými hráči).

Základní informace o varianci, ale i o způsobu, jak změřit štěstí a smůlu, najdete na stránce Variance a $ EV Adjusted. V tomto článku si význam a výpočet variance blíže ukážeme na jednoduchých příkladech krok za krokem s podrobnými komentáři. Poté si můžete prohlédnout další příklad, kde je výpočet variance aplikován přímo na poker, konkrétně na miniturnaj Sit and Go pro 9 hráčů. Je-li variance pro vás novinkou, články vás určitě obohatí.

Příklad aneb jak pochopit varianci

Představte si, že bychom vzali obyčejnou minci a zahráli si s ní následující dvě hry.

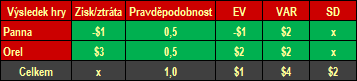
První hra: budu házet mincí. Padne-li orel, dostanu tři dolary ($3), padne-li panna, zaplatím vám jeden dolar (−$1). Že je to pro mě výhodný byznys je na první pohled očividné, ale k pointě příkladu se ještě dostaneme. Ještě dodatek, mohli bychom hrát i o koruny, ale americký dolar jsme zvolili úmyslně, neboť v pokeru se většinou hraje s touto měnou.

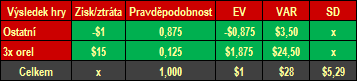
Druhá hra: budu opět házet mincí, ale aby to bylo zajímavější, tentokrát budu muset hodit třikrát po sobě orla. Pokud se mi to povede, dostanu od vás patnáct dolarů ($15). V opačném případě zaplatím jeden dolar (−$1) za každý neúspěšný pokus (tzn., hodím hned pannu, nebo jednou orla, pak pannu, nebo dvakrát po sobě orla a pak to zkazí panna).

1. Výpočet očekávaného výdělku (EV)

Vidíme, že u druhé hry již není tak snadné určit, jestli je pro mě výhodná, či nikoliv. Rozsoudit, která hra je z dlouhodobého pohledu lepší, nám pomůže očekávaná hodnota (EV), což je jakýsi střední odhad (dlouhodobý průměr) výdělečnosti obou her. K tomu ještě potřebujeme určit pravděpodobnosti výhry a prohry v obou hrách a jimi pak vážíme (násobíme) možné zisky či ztráty.

V rychlosti: u první hry je pravděpodobnost výhry „padesát na padesát“, tedy shodně (1/2) = 0,5. Abych vyhrál v druhé hře, musím třikrát po sobě hodit orla. Jelikož pravděpodobnost hodu jednoho orla je 0,5, a jelikož při navazujících pokusech se mezi sebou násobí, pak pravděpodobnost, že hodím orla třikrát po sobě, je 0,5 × 0,5 × 0,5 = 0,125 (nebo 12,5 %, chcete-li). Pravděpodobnost prohry je pak zbytek do jedné (sta procent), tedy 0,875 (či 87,5 %).

Pokud vás zajímá, jak by se například spočítala pravděpodobnost, že z 10 hodů mincí padne 3krát orel, prohlédněte si stránku binomické rozdělení, kde najdete vysvětlení, vzorce i názorné příklady.

Nyní můžeme spočítat očekávanou ziskovost (EV) u obou her:

1. hra: EV = 0,5 × $3 + 0,5 × (−$1) = $1,5 − $0,5 = $1.

2. hra: EV = 0,125 × $15 + 0,875 × (−$1) = $1,875 − $0,875 = $1.

Ještě jednou, co výpočty znamenají: pravděpodobnost výhry krát zisk + pravděpodobnost prohry krát ztráta se záporným znaménkem.

Z výpočtů plyne hned několik věcí. Za prvé, očekávaný výdělek je kladný (+EV), proto jsou pro mě obě hry z dlouhodobého pohledu výhodné. Pokud našel někoho, kdo by byl ochoten je se mnou hrát, pak bych v průměru vydělával 1 dolar z každého hodu (pozn.: u druhé hry můžeme mluvit spíše o jednom pokusu, resp. považovat vrhnutí tří orlů po sobě jako jeden hod/pokus, stejně jako každý neúspěšný pokus).

2. Výpočet variance (VAR)

To, že vyšla EV u obou her stejná ($1) je úmysl, příklad je takto schválně nastaven. Můžeme však cítit, že první hra je určitým způsobem stabilnější, a že ve druhé hře bude spíše docházet k výkyvům ve výdělcích. A o tom je právě variance (VAR). Ukazuje nám, jak mohou být hodnoty rozptýleny okolo EV, ať už na záporné, nebo na kladné straně. Pojďme varianci spočítat, opět nejde o nic až tak složitého, pomůže snad vysvětlující komentář pod výpočty.

1. hra: VAR = 0,5 × ($3 − $1)2 + 0,5 × (−$1 − $1)2 = $4.

2. hra: VAR = 0,125 × ($15 − $1)2 + 0,875 × (−$1 − $1)2 = $28.

A hned se u výpočtu variance zastavme. Co vůbec uvedené výpočty variance představují a znamenají? Varianci (rozptyl) vypočítáme tak, že od každé hodnoty (zisku, nebo ztráty) odečteme střední hodnotu (průměr, EV). Tím tedy zjistíme, jak moc se liší od střední hodnoty.

U první hry jsou to výrazy ($3 − $1) a (−$1 − $1). Dále tyto výrazy umocníme na druhou: ($3 − $1)2 a (−$1 − $1)2. A nakonec oba výrazy vynásobíme pravděpodobnostmi, které slouží jako určitá váha – v první hře jsou stejné, takže bychom je mohli i vynechat, ale ve druhé hře již odlišné pravděpodobnosti výhry a prohry hrají roli. Proč jsme vůbec rozdíly hodnot a průměru (EV) umocňovaly na druhou? Jednoduše proto, aby se navzájem neeliminovaly kladné a záporné hodnoty. Podívejme se, co by se stalo, kdyby rozdíly jednotlivých hodnot (zisku/ztráty) a EV u první hry umocněny nebyly:
VAR = 0,5 × ($3 − $1) + 0,5 × (−$1 − $1) = 0,5 × $2 + 0,5 × (−$2) = $1 − $1 = $0.
To by naznačovalo, že variance (rozptyl hodnot okolo středu) je nulová, což není pravda.

3. Určení směrodatné odchylky (SD) z variance (VAR)

Odchylku od střední hodnoty EV určuje další (a zde poslední) statistika zvaná směrodatná odchylka (SD – z angličtiny Standard Deviation). Směrodatná odchylka (SD) není nic jiného než prostá druhá odmocninou z variance (VAR). Všímáte si souvislostí? Nejprve byly všechny rozdíly jednotlivých hodnot od EV umocněny na druhou, tím se ze záporných čísel stala kladná, a nyní součet všech (kladných) rozdílů odmocníme. Tím získáme (směrodatnou) odchylku od střední hodnoty (EV), která působí na obě strany (+/−).

1. hra: SD = druhá odmocnina z 4$ = $2.

2. hra: SD = druhá odmocnina z 28$ = $5,29.

Praktické využití výpočtů variance

Jak využijeme obecné znalosti a konkrétní výpočty očekávané výdělečnosti (EV), variance (VAR) a odchylky (SD) od střední hodnoty? Nejprve si udělejme malou rekapitulaci, ke které se případně můžete vracet.

Tabulka 1: Shrnutí údajů o první hře s mincí

Variance u první hry s mincí – EV, VAR, SD

Tabulka 2: Shrnutí údajů u druhé hry s mincí

Variance u druhé hry s mincí – EV, VAR, SD

Odehrajme cvičně 100 her, co se stane

Představte si, že se rozhodneme odehrát 100 her (hodů / pokusů). Jestliže očekáváme výdělek jednoho dolaru z každé hry, pak ve sto hrách bychom měli v průměru vydělat 100 dolarů. Úmyslně píšeme „měli vydělat“, protože 100 her, jak bude vidět, nelze považovat za dostatečně velký počet her, aby se ziskovost (téměř) zaručeně projevila.

1. hra:

EV = 1$ × 100 her = $100
VAR = $4 × 100 her = $400
SD = druhá odmocnina ze $400 = $20

Poznámka: SD se dá spočítat také jako druhá odmocnina z ($4 × 100), tedy druhá odmocnina ze $4 krát druhá odmocnina ze 100 her = $2 × 10 = $20.

2. hra:

EV = 1$ × 100 her = $100
VAR = $28 × 100 her = $2800
SD = druhá odmocnina ze $2800 = $53

Jak zacházet s odchylkou

Nyní vstupuje do hry tzv. pravidlo 3 SIGMA. Opět se není čeho obávat. Sigma (σ) je řecké písmeno, kterým se ve statistice označuje směrodatná odchylka (SD) a výrazem σ2 se označuje variance (VAR). My se budeme držet zavedených zkratek SD a VAR na této stránce, i když jde prakticky o totéž. Pravidlo 3 SIGMA nám říká, že:

Zajímat nás budou především poslední dva intervaly, tj. 95 % a 99 %. K čemu slouží? To bude opět jasně patrné z následujících výpočtů a komentářů.

1. hra (zopakujme):

EV = 1$ × 100 her = $100
VAR = $4 × 100 her = $400
SD = druhá odmocnina ze $400 = $20

95 %
min = EV − 2 × SD = $100 − 2 × $20 = $60
max = EV + 2 × SD = $100 + 2 × $20 = $140

Co z toho vyplývá? Při 100 odehraných hrách budu očekávat zisk $100 (EV). A s 95procentní pravděpodobností dosáhnu nejhoršího výsledku +$60 (downswing), za to kdybych měl štěstí (upswing), tak můžu vydělat až +$140.

Budu-li chtít zvýšit míru pravděpodobnosti na 99 %, musím počítat s tím, že i interval se zvětší.

99 %
min = EV − 3 × SD = $100 − 3 × $20 = $40
max = EV + 3 × SD = $100 + 3 × $20 = $160

A opět mohu učinit následující závěr. Při 100 odehraných hrách budu zase očekávat zisk $100 (EV). To je pořád stejné. A s 99procentní pravděpodobností skončím nejhůře 40 dolarů v plusu (kdybych měl smůlu), ale pokud bych měl štěstí, můžu vydělat až 160 dolarů.

To je právě variance a je nutné si uvědomit, že působí oběma směry (do plusu i do minusu). Tato první hra s mincí, kdy dostanu 3 dolary a platím jen 1 dolar při stejné pravděpodobnosti na výhru a prohru, je natolik výhodná, že 100 her stačí k tomu, abych byl na 99 % v plusu. Podívejme se na druhou hru, kde je větší variance.

2. hra (zopakujme):

EV = 1$ × 100 her = $100
VAR = $28 × 100 her = $2800
SD = druhá odmocnina ze $2800 = $53

95 %
min = EV − 2 × SD = $100 − 2 × $53 = −$6
max = EV + 2 × SD = $100 + 2 × $53 = $206

Při 100 odehraných hrách budu rovněž očekávat zisk $100 (EV), ten je stejný ve všech případech a u obou her. Všimněte si ale podstatného rozdílu oproti první hře s mincí. U druhé hry se můj výdělek bude s pravděpodobností 95 % nacházet v intervalu −$6 až +$206. To znamená, že kdybych chytl downswing, mohl bych dokonce prodělat, i když je předpoklad, že v dlouhém období bych měl vydělávat v průměru 1 dolar z každé odehrané hry! Na druhou stranu, při upswingu bych mohl vydělat až 206 dolarů (oproti předpokládaným 100 dolarům).

99 %
min = EV − 3 × SD = $100 − 3 × $53 = −$59
max = EV + 3 × SD = $100 + 3 × $53 = $259

Jaký je závěr pro interval, který pokrývá 99 % hodnot? Při sto odehraných hrách, se můj výdělek bude s pravděpodobností 99 % nacházet v rozmezí minus 59 dolarů až plus 259 dolarů. Pokud budu mít smůlu (downswing), můžu tedy prodělat až 59 dolarů. Pokud by mi přálo mimořádné štěstí (upswing), mohl bych docílit zisku až 259 dolarů. Obojí oproti předpokládanému zisku 100 dolarů ze 100 her.

Co mohu udělat, abych s 99procentní pravděpodobností minimálně neprodělal?

Má strategie, resp. provozování hry je pro mě výhodné, neboť čísla hrají pro mě a dle předpokladu bych měl v průměru vydělávat 1 dolar za každou odehranou hru. Sto her se však ukázalo jako málo, má výhoda se nemusí plně projevit a můžu dokonce skončit v záporu. Řešením je navýšení počtu odehraných her! Čím víc, tím líp. Od jistého bodu prakticky nemohu prodělat, a čím déle budu hru provozovat, tím více se budu blížit k zisku 1 dolar z každé odehrané hry. S větším počtem her bude možný negativní dopad variance potlačen.

Kolik her potřebuji k tomu, abych s 99procentní pravděpodobností neprodělal?

Zlom nastane u počtu her (označme n), kdy je zisk nulový při nejhorším možném průběhu. Jinými slovy, když je dolní hranice intervalu nulová (min = 0). Podmínka je tedy:

n × EV − 3 × druhá odmocnina z (n × VAR) = 0. EV a VAR v tomto vzorci jsou jednotkové, násobí se počtem her n. Po úpravách získáme minimální počet her n, který je potřeba odehrát:

n = 9 × VAR ÷ EV2 a po dosazení

n = 9 × $28 ÷ $12 = 252 her.

Minimálně je třeba odehrát 252 her, aby byl zisk z provozování druhé hry s mincí minimálně na nule (při nejhorším možném průběhu hry – downswingu). Ověřme:

2. hra, 252 her

EV = 1$ × 252 her = $252
VAR = $28 × 252 her = $7056
SD = druhá odmocnina ze $7056 = $84

99 %
min = EV − 3 × SD = $252 − 3 × $84 = $0
max = EV + 3 × SD = $252 + 3 × $84 = $504

Závěr

Dvě jednoduché hry s mincí demonstrovaly význam variance (rozptylu) nejen v pokeru. Obě hry by byly pro provozovatele výhodné, neboť by mu přinesly shodný dlouhodobý průměrný zisk jeden dolar z každé odehrané hry. Samozřejmě to neznamená, že každá jednotlivá hra (hod mincí) by skončil tímto výsledkem, ale že v dlouhém období, tj. po dostatečně velkém počtu odehraných her, by výdělečnost provozovatele her k tomuto výsledku směřovala.

Výsledky hráče v dlouhém období mají tendenci pohybovat v blízkosti průměru. V krátkém období však může docházet k odchylkám. Variance ukazuje, jak velké tyto odchylky mohou být. Čím vyšší variance (odchylka), tím vyšší riziko, že se pokerový hráč může dostat do minusu. Variance však působí oběma směry a je možné i více vydělat (rozpětí min-max).

Provozovatel hry, která má kladnou očekávanou hodnotu (+EV), nebo pokerový hráč, který má dobrou strategii, resp. hraje dobře poker a má dlouhodobou ziskovost (+EV či +ROI), musí při dostatečně velkém počtu her nakonec vydělat, resp. být v plusu. Druhá hra s mincí ukázala, že čím vyšší je variance, tím větší počet her je třeba odehrát, aby se strategie/výhoda projevila zaručeně, resp. s vysokou mírou pravděpodobnosti (95 či 99 %). Je žádoucí usilovat o co nejvyšší EV a o co nejnižší VAR.

Pokud podnikáte, operujete s prodeji nebo investujete do akcií, můžete se pod prvními dvěma odkazy podívat na to, jak lze využít očekávanou hodnotu a varianci (ta ukazuje riziko) v těchto oblastech. Princip je naprosto stejný jako u her na této stránce.

Kam dál:

EN Variance Example – tento článek v angličtině.